Using ASCII waveforms to test real-time audio code

I draw sound wave ASCII art in Q2Q’s source code. These ASCII art waveforms ensure that the real-time audio engine at the heart of Q2Q stays bug-free.

Software development best-practices dictate that if you want your software to be high-quality (who doesn’t?), you test your code, you test it automatically, and you test it often (as part of a continuous integration build process). In other words, you should make accidentally publishing bugs as difficult as possible. Q2Q, of course, has test suites to prevent regressions, and a CI system that makes sure all tests pass (just like any other good software project).

Q2Q is a real-time audo application. It does things like starting/stopping sounds, fading/panning sounds, and looping/devamping sounds, and these kinds of features are mission-critical. They cannot fail or have bugs. Here’s the catch: audio programming is extremely tricky to get right. When I was first writing Q2Q, I spent days trying to get anything coherent out of the speakers even at all. It’s very easy to get some buffer index wrong, or do a time conversion incorrectly, or forget to handle more than just mono and stereo signals, or even to just be off by a small number of samples without noticing.

This is hard to write automated tests for – how are you supposed to write a test that asserts, “a one-second fade-out should work”? My initial thought was to take a sliding average (approximating loudness), and assert that it constantly decreases, for example. But then how would you test looping functionality? Or mixing different sounds together? Or crossfading? Trying to come up with how to test those invariants is very hard.

I stumbled across a post from Jane Street’s tech blog that describes a technique for testing hardware oscillators (which generate waveforms), where they render the oscillator’s output to text, which can be very easilly diffed. Additionally, the F# compiler has some tests (which it calls “baseline tests”) that test the new compiler’s output against output from an earlier known-good version of itself. A combination of these two approaches sounded very good to me.

Q2Q employs this ASCII-waveform baseline testing technique to great success. Every time I work on a new feature, I manually create some test cases for the new feature. For example, if I were writing the component that performs fading and panning, I would first create a test case to exercise a simple fade (perhaps a short fade-out), and output to a simple array, instead of an actual output device (this is pretty easy as I use NAudio for audio processing). Then, I would attempt to implement the feature. Then, I would use my ASCIIWaveformRenderer to turn the output into an array of strings, acting as a visual representation of the data that would have been outputted to the audio device. I would run this in F# interactive, so that if it looks good, I can copy-paste the result right back into the test code as the baseline to compare against from now on. If it didn’t look right, I would tweak the code until it does. Rinse and repeat for all the corner cases.

Fade-in baseline test using an ASCII waveform.

A baseline test for a looping using slices. Notice how the slicer first plays straight through a signal, then loops the last part of the waveform.

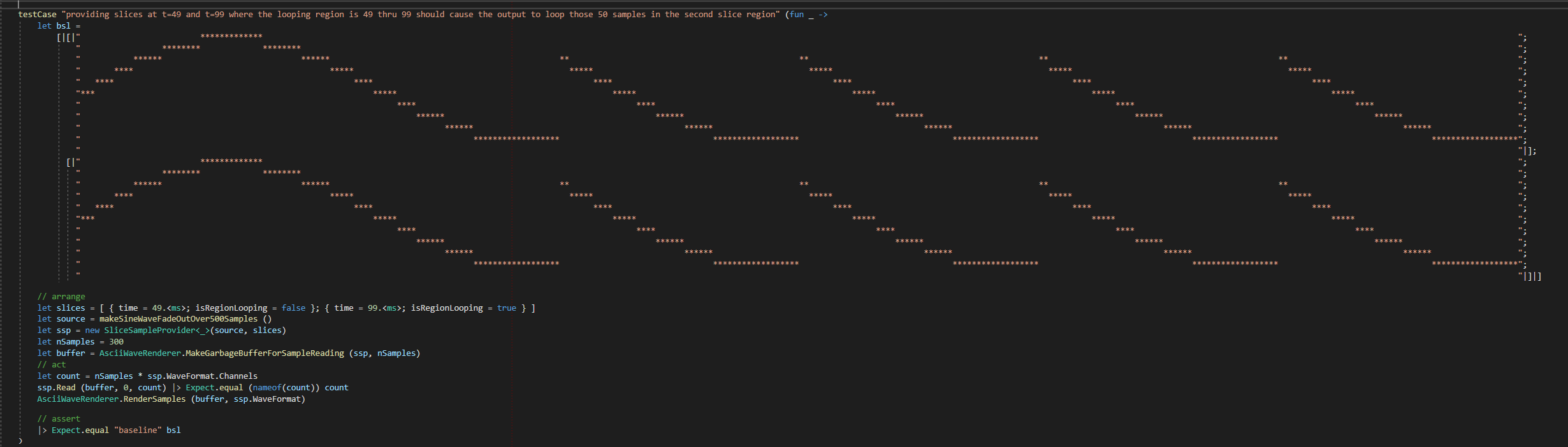
This provides a great regression testing experience. Recently, while implementing pan laws, I noticed that the CI had started failing. I opened up the error log and was greeted with this:

ASCII waveform baseline test failure.

This is telling us that a test is failing because the system’s output did not match the expected ASCII waveform baseline.

The tests for FadeSampleProvider (the component that handles fading and panning), were catching a legitimate mistake. As you can see, storing the baseline as an ASCII waveform makes this much easier to debug than if it were to be an opaque array of raw sample data. Expecto, the test framework I use, even gives a good enough visual diff there. You can kind of tell what is going wrong just by the picture – it’s supposed to be a fade out, as indicated by the first (green) waveform (so gradually decreasing in overall volume), and it kind of does this at first, but then the signal starts fading back in! Why was this happening? After some digging, it turns out that I had accidentally removed the clamping logic in the interpolation functions, thinking they were do-nothing code. These interpolations are simply mathematical functions¹, so you can put in numbers you would consider invalid, and they will happily start doing funny things – like causing a fade-out to start fading back in. Oops!

The interesting thing is that if these tests weren’t around, this bug probably would have gone unidentified, causing subtle glitches, for quite a while. Since the audio is streamed in real time, it is not processed all at once; rather, it is processed in buffered chunks. When the audio device is ready for more sound to play, it gives Q2Q an empty buffer, which Q2Q then fills with samples from the processing chain. This happens many time per second (as determined by the size of the buffer). FadeSampleProvider only calls the interpolation function when a fade is actually in progress – but it only re-decides this on the next buffer. Therefore, when a fade ends before the end of the buffer (which it likely would), it would exhibit this problem for the rest of that audio buffer. Buffer sizes are small enough (as measure in seconds) that it likely would have sounded like a millisecond-long click or pop, which would have been extremely difficult to attribute to the FadeSampleProvider in particular. I would have probably chalked it up to slow file reading, or inefficient code causing the device to drop some frames.

ASCII-waveform baseline tests are great, but what about the cases I don’t know to write tests for? Can we take this even further? Check back for a future blog post – Property-based fuzz testing to the rescue!

EDIT: since people were interested, I’ve posted the waveform-to-ASCII renderer as a snippet free to use: http://www.fssnip.net/85g

1. I use different kinds of interpolation functions to implement the different fade shapes you can use, such as linear fades, constant-power fades, and compromise fades. Here’s a sample graph of some of these functions plotted together, and here’s that same graph without restricting the x axis to a specific range. Observe that the output makes sense as a fade volume for x values from 0 to 1, but start to get weird outside of that range. Hence, we need to clamp the x value between 0 and 1 before we pass it into the interpolation formula. ↩